15. Taylor Diagrams
15.1. Description
Taylor diagrams are used to show a relationship between continuous statistics (Taylor, 2001). This type of plot is used to quantify the degree of correspondence between the forecasts and observations with respect to three continuous statistics: the Pearson correlation coefficient, the root-mean-square error (RMSE), and the standard deviation. This output can be produced by many of the MET tools (Point-Stat, Grid-Stat, etc.) via the continuous statistics line type. In METviewer, continuous statistics can be accumulated over some time period but kept separate for different models, lead times, observation sources, domains, etc.
The distance between each forecast and the observation on the graph is a measure of how realistically each forecast reproduces that observation. For each forecast, three statistics are plotted: the Pearson correlation coefficient (Wilks, 2011; a measure of pattern similarity between the forecast and observed fields) is related to the azimuthal angle; the normalized (bias-corrected) RMSE in the forecast field is proportional to the distance from the point on the x-axis identified as “observed”. The standard deviation of the forecast is proportional to the radial distance from the origin. The means of the fields are subtracted out before computing their second-order statistics (e.g. bias-corrected RMSE), so the diagram does not provide information about biases. Rather, it characterizes the pattern error.
So, better forecasts lie closer on the Taylor diagram to observation point, while worse forecasts lie further away.
15.2. Line Type
Taylor requires continuous statistics, CNT, generated by either Point-Stat or Grid-Stat.
15.3. How-To
Selection of options to produce the Taylor diagram proceeds approximately counter-clockwise around the METviewer window.
Select the desired database from the “Select databases” pulldown menu at the top margin of the METviewer window.
There are a number of tabs just under the database pulldown menu. Select the ‘Taylor’ tab.
Select the dependent variable to calculate statistics for in the “Y1 Dependent (Forecast) Variables” tab. The first pulldown menu in the “Y1 Dependent (Forecast) Variables” section lists the variables available in the selected database.
Select the Y1 Series Variable from the first pulldown menu in that section. There are many options. The example below uses two series variables, “MODEL” and “VX_MASK”. In the second pulldown menu to the right of the first are the series variable options, for example, different models.
It usually does not make sense to mix statistics for different groups. The desired group to calculate statistics over can be specified in the “Fixed Values” section. If multiple domains or thresholds were chosen, the statistics would be a summary of all of those cases together, which may not always be desired.
Choose the display option in the “Display” section. There are two options.
Values of Correlation: Select to show only positive correlation values or show all correlation values.
Standard Deviation Arcs: Select whether to display or hide the standard deviation arcs.
Now enough information has been entered to produce a graph. To do this, click the “Generate Plot” button at the top of the METviewer window (this is in red text). Typically, if a plot is not produced, it is because the database selected does not contain the correct type of data. Also, it is imperative to check the data used for the plot by selecting the “R data” tab on the right hand side, above the plot area. The data from the database that is being used to calculate the statistics is listed in this tab. This tab should be checked to avoid the accidental accumulation of inappropriate database lines. For example, it does not make sense to accumulate statistics over different domains, thresholds, models, etc.
There are many other options for plots, but these are the basics.
15.4. Example
The example Taylor diagram below shows the downward longwave radiation flux (DLWRF) correlation and standard deviation for one model and seven locations. The model forecast performs well for the Bondville and Fort Peck locations. The Bondville location has the best value of 0.85 correlation and near 1 values of standard deviation. The ideal value is 1, which corresponds to perfect correlation and matching standard deviations between model and observation.
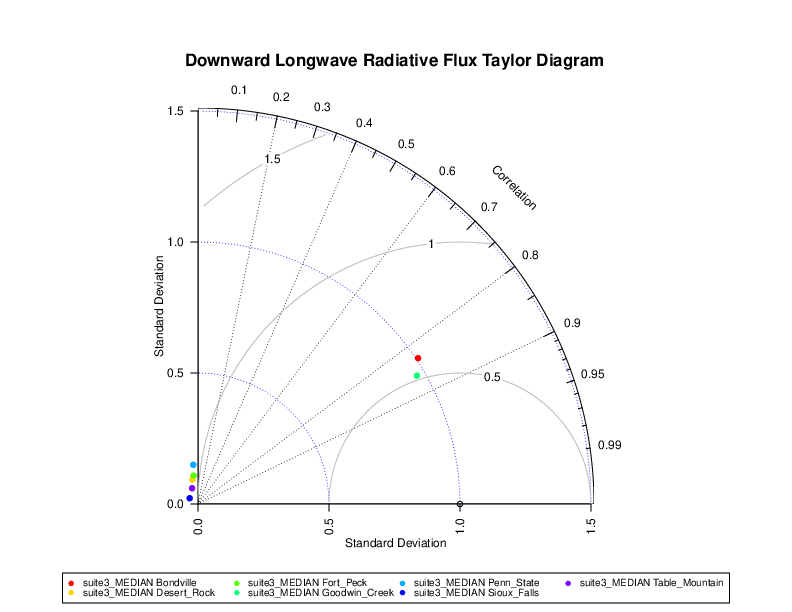
Figure 15.1 Example Taylor diagram.
Here is the associated xml for this example. It can be copied into an empty file and saved to the desktop then uploaded into the system by clicking on the “Load XML” button in the upper-right corner of the GUI. This XML can be downloaded from this link: taylor_diagram.xml
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<plot_spec>
<connection>
<host>mohawk</host>
<database>mv_gmtb_surfrad</database>
<user>******</user>
<password>******</password>
<management_system>mariadb</management_system>
</connection>
<rscript>/usr/local/R/bin/Rscript</rscript>
<folders>
<r_tmpl>/opt/vxwww/tomcat/webapps/metviewer//R_tmpl</r_tmpl>
<r_work>/opt/vxwww/tomcat/webapps/metviewer//R_work</r_work>
<plots>/d2/www/dtcenter/met/metviewer_output//plots</plots>
<data>/d2/www/dtcenter/met/metviewer_output//data</data>
<scripts>/d2/www/dtcenter/met/metviewer_output//scripts</scripts>
</folders>
<plot>
<template>taylor_plot.R_tmpl</template>
<dep>
<dep1>
<fcst_var name="DLWRF"/>
</dep1>
</dep>
<series1>
<field name="model">
<val>suite3_MEDIAN</val>
</field>
<field name="vx_mask">
<val>Bondville</val>
<val>Desert_Rock</val>
<val>Fort_Peck</val>
<val>Goodwin_Creek</val>
<val>Penn_State</val>
<val>Sioux_Falls</val>
<val>Table_Mountain</val>
</field>
</series1>
<plot_fix/>
<plot_cond/>
<taylor_voc>true</taylor_voc>
<taylor_show_gamma>true</taylor_show_gamma>
<tmpl>
<data_file>plot_20200924_220648.data</data_file>
<plot_file>plot_20200924_220648.png</plot_file>
<r_file>plot_20200924_220648.R</r_file>
<title>Downward Longwave Radiative Flux Taylor Diagram</title>
<x_label>Standard Deviation</x_label>
<y1_label>Standard Deviation</y1_label>
<y2_label/>
<caption/>
<job_title/>
<keep_revisions>false</keep_revisions>
<listdiffseries1>list()</listdiffseries1>
<listdiffseries2>list()</listdiffseries2>
</tmpl>
<execution_type>Rscript</execution_type>
<event_equal>false</event_equal>
<vert_plot>false</vert_plot>
<x_reverse>false</x_reverse>
<num_stats>false</num_stats>
<indy1_stag>false</indy1_stag>
<indy2_stag>false</indy2_stag>
<grid_on>true</grid_on>
<sync_axes>false</sync_axes>
<dump_points1>false</dump_points1>
<dump_points2>false</dump_points2>
<log_y1>false</log_y1>
<log_y2>false</log_y2>
<varianceinflationfactor>false</varianceinflationfactor>
<plot_type>png16m</plot_type>
<plot_height>8.5</plot_height>
<plot_width>11</plot_width>
<plot_res>72</plot_res>
<plot_units>in</plot_units>
<mar>c(8,4,5,4)</mar>
<mgp>c(1,1,0)</mgp>
<cex>1</cex>
<title_weight>2</title_weight>
<title_size>1.4</title_size>
<title_offset>-2</title_offset>
<title_align>0.5</title_align>
<xtlab_orient>1</xtlab_orient>
<xtlab_perp>-0.75</xtlab_perp>
<xtlab_horiz>0.5</xtlab_horiz>
<xtlab_freq>0</xtlab_freq>
<xtlab_size>1</xtlab_size>
<xlab_weight>1</xlab_weight>
<xlab_size>1</xlab_size>
<xlab_offset>2</xlab_offset>
<xlab_align>0.5</xlab_align>
<ytlab_orient>1</ytlab_orient>
<ytlab_perp>0.5</ytlab_perp>
<ytlab_horiz>0.5</ytlab_horiz>
<ytlab_size>1</ytlab_size>
<ylab_weight>1</ylab_weight>
<ylab_size>1</ylab_size>
<ylab_offset>-2</ylab_offset>
<ylab_align>0.5</ylab_align>
<grid_lty>3</grid_lty>
<grid_col>#cccccc</grid_col>
<grid_lwd>1</grid_lwd>
<grid_x>listX</grid_x>
<x2tlab_orient>1</x2tlab_orient>
<x2tlab_perp>1</x2tlab_perp>
<x2tlab_horiz>0.5</x2tlab_horiz>
<x2tlab_size>0.8</x2tlab_size>
<x2lab_size>0.8</x2lab_size>
<x2lab_offset>-0.5</x2lab_offset>
<x2lab_align>0.5</x2lab_align>
<y2tlab_orient>1</y2tlab_orient>
<y2tlab_perp>0.5</y2tlab_perp>
<y2tlab_horiz>0.5</y2tlab_horiz>
<y2tlab_size>1</y2tlab_size>
<y2lab_size>1</y2lab_size>
<y2lab_offset>1</y2lab_offset>
<y2lab_align>0.5</y2lab_align>
<legend_box>o</legend_box>
<legend_inset>c(0, -.25)</legend_inset>
<legend_ncol>4</legend_ncol>
<legend_size>0.8</legend_size>
<caption_weight>1</caption_weight>
<caption_col>#333333</caption_col>
<caption_size>0.8</caption_size>
<caption_offset>3</caption_offset>
<caption_align>0</caption_align>
<ci_alpha>0.05</ci_alpha>
<plot_ci>c("none","none","none","none","none","none","none")</plot_ci>
<show_signif>c(TRUE,TRUE,TRUE,TRUE,TRUE,TRUE,TRUE)</show_signif>
<plot_disp>c(TRUE,TRUE,TRUE,TRUE,TRUE,TRUE,TRUE)</plot_disp>
<colors>c("#ff0000FF","#ffd400FF","#55ff00FF","#00ff7fFF","#00aaffFF","#1500ffFF","#7f00ffFF")</colors>
<pch>c(19,19,19,19,19,19,19)</pch>
<type>c("b","b","b","b","b","b","b")</type>
<lty>c(1,1,1,1,1,1,1)</lty>
<lwd>c(5,5,5,5,5,5,5)</lwd>
<con_series>c(1,1,1,1,1,1,1)</con_series>
<order_series>c(1,2,3,4,5,6,7)</order_series>
<plot_cmd/>
<legend>c("","","","","","","")</legend>
<y1_lim>c()</y1_lim>
<x1_lim>c()</x1_lim>
<y1_bufr>0.04</y1_bufr>
<y2_lim>c(0,1)</y2_lim>
</plot>
</plot_spec>